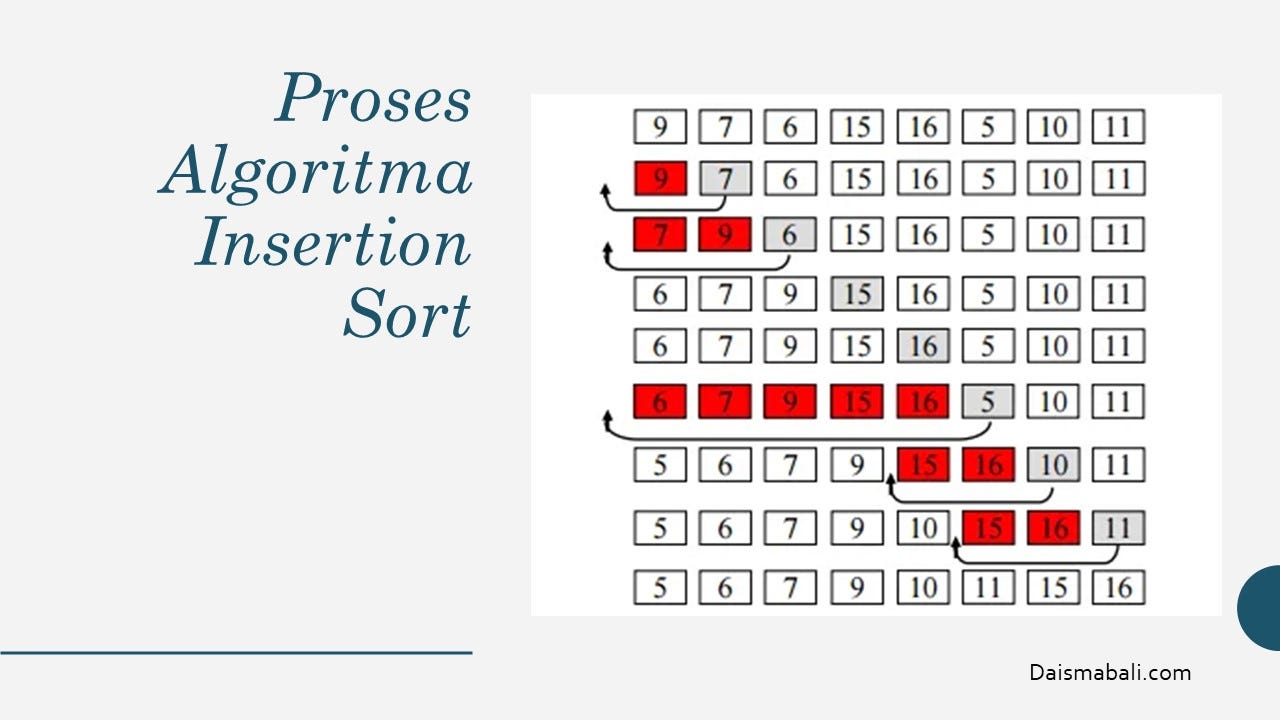
Array dalam C++
Array adalah struktur data yang digunakan untuk menyimpan sekumpulan elemen yang memiliki tipe data yang sama dalam satu variabel. Dalam C++, array memungkinkan kita untuk mengakses dan memanipulasi data dengan lebih efisien menggunakan indeks. Berikut adalah penjelasan mendalam tentang array, beserta contoh sintaks dan latihan soal:
Penjelasan Array
Deklarasi Array: Untuk mendeklarasikan array di C++, Anda perlu menentukan tipe data elemen array dan ukuran array. Contohnya:
int arr[5];Ini mendeklarasikan sebuah array
arrdengan 5 elemen yang bertipeint.Inisialisasi Array: Anda bisa menginisialisasi array saat mendeklarasikannya atau setelah deklarasi. Contohnya:
int arr[5] = {1, 2, 3, 4, 5}; // Inisialisasi saat deklarasi int arr[5]; arr[0] = 1; arr[1] = 2; arr[2] = 3; arr[3] = 4; arr[4] = 5; // Inisialisasi setelah deklarasiMengakses Elemen Array: Elemen array diakses menggunakan indeks, yang dimulai dari 0. Contohnya:
int x = arr[0]; // Mengakses elemen pertama arr[1] = 10; // Mengubah nilai elemen keduaUkuran Array: Ukuran array harus ditentukan saat deklarasi dan tidak bisa diubah setelah itu. Anda dapat menggunakan
sizeofuntuk mengetahui ukuran total array dalam byte:int size = sizeof(arr) / sizeof(arr[0]); // Menghitung jumlah elemen
Contoh Sintaks C++
Berikut adalah contoh program C++ sederhana yang menggunakan array:
#include <iostream>
using namespace std;
int main() {
// Deklarasi dan Inisialisasi Array
int numbers[5] = {10, 20, 30, 40, 50};
// Mengakses dan Menampilkan Elemen Array
for(int i = 0; i < 5; i++) {
cout << "Element at index " << i << " is " << numbers[i] << endl;
}
// Mengubah Nilai Elemen Array
numbers[2] = 100;
// Menampilkan Elemen Array setelah perubahan
cout << "After modification:" << endl;
for(int i = 0; i < 5; i++) {
cout << "Element at index " << i << " is " << numbers[i] << endl;
}
return 0;
}
Element at index 0 is 10
Element at index 1 is 20
Element at index 2 is 30
Element at index 3 is 40
Element at index 4 is 50
After modification:
Element at index 0 is 10
Element at index 1 is 20
Element at index 2 is 100
Element at index 3 is 40
Element at index 4 is 50
Latihan Soal
Latihan 1: Buatlah program yang mendeklarasikan array
floatdengan 4 elemen, inisialisasi dengan nilai-nilai acak, dan cetak setiap elemen serta rata-ratanya.Latihan 2: Tulis program yang mendeklarasikan array
intdengan 6 elemen, inisialisasi dengan nilai-nilai dari 1 hingga 6. Buatlah fungsi untuk menghitung jumlah dan rata-rata dari elemen-elemen array tersebut.Latihan 3: Buatlah program yang mendeklarasikan array dua dimensi
3x3(matriks) dan inisialisasi dengan angka-angka dari 1 hingga 9. Tampilkan matriks tersebut dalam format tabel.
Solusi Latihan
Latihan 1:
#include <iostream>
using namespace std;
int main() {
float numbers[4] = {5.6, 3.4, 7.8, 1.2};
float sum = 0;
for(int i = 0; i < 4; i++) {
sum += numbers[i];
}
cout << "Elements of the array:" << endl;
for(int i = 0; i < 4; i++) {
cout << numbers[i] << " ";
}
cout << endl;
cout << "Average: " << sum / 4 << endl;
return 0;
}
Latihan 2:
#include <iostream>
using namespace std;
void calculateSumAndAverage(int arr[], int size, int &sum, float &average) {
sum = 0;
for(int i = 0; i < size; i++) {
sum += arr[i];
}
average = static_cast<float>(sum) / size;
}
int main() {
int numbers[6] = {1, 2, 3, 4, 5, 6};
int sum;
float average;
calculateSumAndAverage(numbers, 6, sum, average);
cout << "Sum: " << sum << endl;
cout << "Average: " << average << endl;
return 0;
}
Latihan 3:
#include <iostream>
using namespace std;
int main() {
int matrix[3][3] = {
{1, 2, 3},
{4, 5, 6},
{7, 8, 9}
};
cout << "Matrix:" << endl;
for(int i = 0; i < 3; i++) {
for(int j = 0; j < 3; j++) {
cout << matrix[i][j] << " ";
}
cout << endl;
}
return 0;
}
Berikut adalah beberapa contoh penggunaan array
dalam konteks kehidupan sehari-hari dan sintaks C++ yang sesuai untuk masing-masing contoh:
1. Menyimpan Skor Nilai Siswa
Misalkan Anda ingin menyimpan skor ujian dari beberapa siswa. Anda bisa menggunakan array untuk menyimpan nilai-nilai tersebut.
#include <iostream>
using namespace std;
int main() {
// Deklarasi dan Inisialisasi Array untuk menyimpan nilai ujian siswa
int scores[5] = {85, 90, 78, 92, 88};
int total = 0;
int numberOfStudents = sizeof(scores) / sizeof(scores[0]);
// Menampilkan nilai setiap siswa
cout << "Scores of the students:" << endl;
for (int i = 0; i < numberOfStudents; i++) {
cout << "Student " << (i + 1) << ": " << scores[i] << endl;
total += scores[i];
}
// Menghitung rata-rata nilai
float average = static_cast<float>(total) / numberOfStudents;
cout << "Average score: " << average << endl;
return 0;
}
2. Menampilkan Jadwal Mingguan
Jika Anda ingin menyimpan jadwal kegiatan harian untuk seminggu, Anda dapat menggunakan array satu dimensi.
#include <iostream>
#include <string>
using namespace std;
int main() {
// Deklarasi dan Inisialisasi Array untuk menyimpan jadwal mingguan
string schedule[7] = {
"Monday: Meeting with team",
"Tuesday: Project work",
"Wednesday: Client call",
"Thursday: Presentation preparation",
"Friday: Weekly review",
"Saturday: Team outing",
"Sunday: Rest day"
};
// Menampilkan jadwal mingguan
cout << "Weekly Schedule:" << endl;
for (int i = 0; i < 7; i++) {
cout << schedule[i] << endl;
}
return 0;
}
3. Mengelola Inventaris Barang
Jika Anda memiliki inventaris barang di sebuah toko dan ingin menyimpan jumlah setiap barang yang tersedia, Anda bisa menggunakan array.
#include <iostream>
using namespace std;
int main() {
// Deklarasi dan Inisialisasi Array untuk menyimpan jumlah inventaris barang
int inventory[4] = {50, 30, 20, 40}; // Misalnya: barang A, B, C, D
string itemNames[4] = {"Item A", "Item B", "Item C", "Item D"};
// Menampilkan jumlah inventaris setiap barang
cout << "Inventory:" << endl;
for (int i = 0; i < 4; i++) {
cout << itemNames[i] << ": " << inventory[i] << " units" << endl;
}
return 0;
}
4. Menangani Suhu Harian
Anda bisa menggunakan array untuk menyimpan data suhu harian dalam satu bulan.
#include <iostream>
using namespace std;
int main() {
// Deklarasi dan Inisialisasi Array untuk suhu harian
float temperatures[30] = {22.5, 21.0, 23.1, 22.8, 24.0, /* ...data lain... */ 21.5}; // Misalkan ada 30 hari data suhu
float sum = 0;
int numberOfDays = sizeof(temperatures) / sizeof(temperatures[0]);
// Menghitung rata-rata suhu
for (int i = 0; i < numberOfDays; i++) {
sum += temperatures[i];
}
float averageTemperature = sum / numberOfDays;
cout << "Average Temperature for the month: " << averageTemperature << " °C" << endl;
return 0;
}
5. Menyimpan Data Kontak
Jika Anda ingin menyimpan nomor telepon dalam sebuah kontak, array dapat digunakan untuk mengelola data tersebut.
#include <iostream>
#include <string>
using namespace std;
int main() {
// Deklarasi dan Inisialisasi Array untuk nomor telepon
string phoneNumbers[3] = {"123-456-7890", "987-654-3210", "555-555-5555"};
string names[3] = {"Alice", "Bob", "Charlie"};
// Menampilkan daftar kontak
cout << "Contact List:" << endl;
for (int i = 0; i < 3; i++) {
cout << names[i] << ": " << phoneNumbers[i] << endl;
}
return 0;
}
Penjelasan Kode:
- Deklarasi Array:
int scores[5], string schedule[7], int inventory[4], float temperatures[30], string phoneNumbers[3] digunakan untuk mendeklarasikan array dengan elemen sesuai kebutuhan. - Inisialisasi Array: Data diisi langsung saat deklarasi atau diisi setelah deklarasi.
- Mengakses Elemen Array: Menggunakan indeks array seperti
scores[i], schedule[i], dll. - Pengulangan Array: Menggunakan loop
for untuk iterasi elemen array.
 Reviewed by fortunez
on
August 23, 2024
Rating:
Reviewed by fortunez
on
August 23, 2024
Rating: