Proses menyusun data dalam urutan tertentu, biasanya berdasarkan nilai atau kriteria tertentu. Pengurutan adalah operasi fundamental dalam ilmu komputer dan banyak digunakan dalam berbagai aplikasi, seperti penyimpanan data, pencarian, dan analisis.
1. Pengurutan Bubble (Bubble Sort)
Deskripsi: Mengulang melalui daftar dan membandingkan pasangan elemen yang berdekatan, menukar mereka jika mereka berada dalam urutan yang salah. Proses ini diulang hingga daftar terurut.
Kompleksitas Waktu: O(n^2)
Contoh Implementasi:
#include <iostream>
using namespace std;
void bubbleSort(int arr[], int n) {
for (int i = 0; i < n-1; i++) {
for (int j = 0; j < n-i-1; j++) {
if (arr[j] > arr[j+1]) {
// Tukar arr[j] dan arr[j+1]
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
}
void printArray(int arr[], int size) {
for (int i = 0; i < size; i++)
cout << arr[i] << " ";
cout << endl;
}
int main() {
int arr[] = {64, 34, 25, 12, 22, 11, 90};
int n = sizeof(arr)/sizeof(arr[0]);
bubbleSort(arr, n);
cout << "Array terurut: ";
printArray(arr, n);
return 0;
}
2. Pengurutan Seleksi (Selection Sort)
Deskripsi: Mencari elemen terkecil (atau terbesar) dari bagian yang belum terurut dan menukarnya dengan elemen pertama dari bagian tersebut.
Kompleksitas Waktu: O(n^2)
Contoh Implementasi:
#include <iostream>
using namespace std;
void selectionSort(int arr[], int n) {
for (int i = 0; i < n-1; i++) {
int minIdx = i;
for (int j = i+1; j < n; j++) {
if (arr[j] < arr[minIdx]) {
minIdx = j;
}
}
// Tukar arr[i] dan arr[minIdx]
int temp = arr[minIdx];
arr[minIdx] = arr[i];
arr[i] = temp;
}
}
void printArray(int arr[], int size) {
for (int i = 0; i < size; i++)
cout << arr[i] << " ";
cout << endl;
}
int main() {
int arr[] = {64, 25, 12, 22, 11};
int n = sizeof(arr)/sizeof(arr[0]);
selectionSort(arr, n);
cout << "Array terurut: ";
printArray(arr, n);
return 0;
}
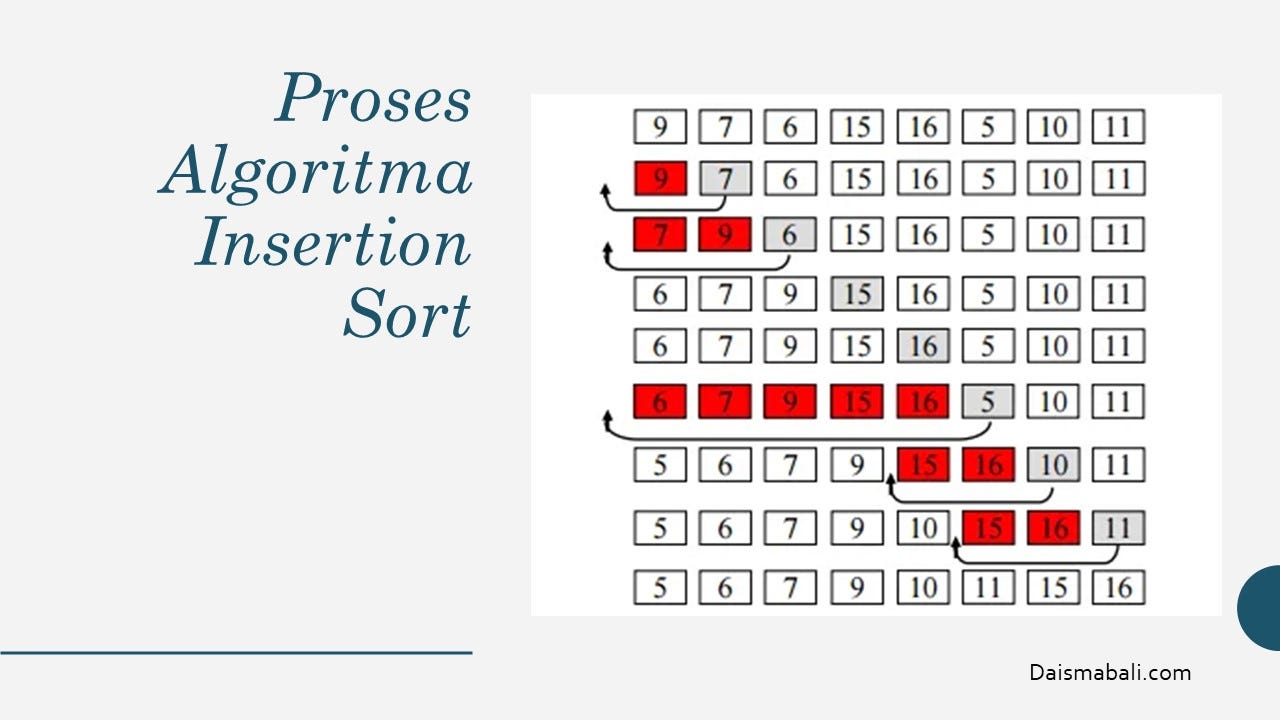
3. Pengurutan Sisip (Insertion Sort)
Deskripsi: Mengambil elemen satu per satu dan menyisipkannya pada posisi yang tepat di bagian yang sudah terurut dari daftar.
Kompleksitas Waktu: O(n^2)
Contoh Implementasi:
#include <iostream>
using namespace std;
void insertionSort(int arr[], int n) {
for (int i = 1; i < n; i++) {
int key = arr[i];
int j = i - 1;
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = key;
}
}
void printArray(int arr[], int size) {
for (int i = 0; i < size; i++)
cout << arr[i] << " ";
cout << endl;
}
int main() {
int arr[] = {64, 34, 25, 12, 22, 11, 90};
int n = sizeof(arr)/sizeof(arr[0]);
insertionSort(arr, n);
cout << "Array terurut: ";
printArray(arr, n);
return 0;
}
4. Pengurutan Merge (Merge Sort)
Deskripsi: Metode pengurutan berbasis pembagian dan penaklukan yang membagi daftar menjadi dua bagian, mengurutkan masing-masing bagian, dan kemudian menggabungkannya.
Kompleksitas Waktu: O(n log n)
Contoh Implementasi:
#include <iostream>
using namespace std;
void merge(int arr[], int l, int m, int r) {
int n1 = m - l + 1;
int n2 = r - m;
int* L = new int[n1];
int* R = new int[n2];
for (int i = 0; i < n1; i++)
L[i] = arr[l + i];
for (int j = 0; j < n2; j++)
R[j] = arr[m + 1 + j];
int i = 0;
int j = 0;
int k = l;
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
} else {
arr[k] = R[j];
j++;
}
k++;
}
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
delete[] L;
delete[] R;
}
void mergeSort(int arr[], int l, int r) {
if (l < r) {
int m = l + (r - l) / 2;
mergeSort(arr, l, m);
mergeSort(arr, m + 1, r);
merge(arr, l, m, r);
}
}
void printArray(int arr[], int size) {
for (int i = 0; i < size; i++)
cout << arr[i] << " ";
cout << endl;
}
int main() {
int arr[] = {38, 27, 43, 3, 9, 82, 10};
int n = sizeof(arr)/sizeof(arr[0]);
mergeSort(arr, 0, n - 1);
cout << "Array terurut: ";
printArray(arr, n);
return 0;
}
5. Pengurutan Quick (Quick Sort)
Deskripsi: Metode pengurutan berbasis pembagian dan penaklukan yang memilih elemen pivot, mengurutkan elemen yang lebih kecil dan lebih besar dari pivot, dan kemudian menggabungkannya.
Kompleksitas Waktu: O(n log n) rata-rata, O(n^2) terburuk
Contoh Implementasi:
#include <iostream>
using namespace std;
int partition(int arr[], int low, int high) {
int pivot = arr[high];
int i = (low - 1);
for (int j = low; j < high; j++) {
if (arr[j] < pivot) {
i++;
swap(arr[i], arr[j]);
}
}
swap(arr[i + 1], arr[high]);
return (i + 1);
}
void quickSort(int arr[], int low, int high) {
if (low < high) {
int pi = partition(arr, low, high);
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
void printArray(int arr[], int size) {
for (int i = 0; i < size; i++)
cout << arr[i] << " ";
cout << endl;
}
int main() {
int arr[] = {10, 7, 8, 9, 1, 5};
int n = sizeof(arr)/sizeof(arr[0]);
quickSort(arr, 0, n - 1);
cout << "Array terurut: ";
printArray(arr, n);
return 0;
}
6. Pengurutan Heap (Heap Sort)
Deskripsi: Menggunakan struktur data heap untuk mengurutkan data dengan membangun heap dari data, lalu mengeluarkan elemen dari heap satu per satu.
Kompleksitas Waktu: O(n log n)
Contoh Implementasi:
#include <iostream>
using namespace std;
void heapify(int arr[], int n, int i) {
int largest = i;
int l = 2 * i + 1;
int r = 2 * i + 2;
if (l < n && arr[l] > arr[largest])
largest = l;
if (r < n && arr[r] > arr[largest])
largest = r;
if (largest != i) {
swap(arr[i], arr[largest]);
heapify(arr, n, largest);
}
}
void heapSort(int arr[], int n) {
for (int i = n / 2 - 1; i >= 0; i--)
heapify(arr, n, i);
for (int i = n - 1; i >= 0; i--) {
swap(arr[0], arr[i]);
heapify(arr, i, 0);
}
}
void printArray(int arr[], int size) {
for (int i = 0; i < size; i++)
cout << arr[i] << " ";
cout << endl;
}
int main() {
int arr[] = {12, 11, 13, 5, 6, 7};
int n = sizeof(arr)/sizeof(arr[0]);
heapSort(arr, n);
cout << "Array terurut: ";
printArray(arr, n);
return 0;
}